Examen Diagnóstico (electrónica digital II)
1. Representa en hexadecimal los siguientes números binarios:
a) 1110 0001 1100 1010 0000 0011 0001
b) 11 1111 0000 1100 1000
a) E1CA031
b) 3F0C8
2. Representa en binario los siguientes números hexadecimales ($ -> representa un número hexadecimal)
a) $212F04
b) $CAFE
a) 0010 0001 0010 1111 0000 0100
b) 1100 1010 1111 1110
3. Calcula el Ca1 (Complemento a 1) y el Ca2 (complemento a 2) de los siguientes números:
a) $3FA
b) 1101112
4. Simplificar la función de Boole F = S (m0, m4, m7, m9) con condiciones de importa, NI = S (m1, m5, m11, m14), utilizando mapas de Karnaugh (recuerde que los minitérminos se marcan con un 1, las condiciones de no importa con una X y las celdas restantes con 0).
5. El Decodificador de 2 a 4 líneas (2 bits) tiene 2 líneas de entrada y 4 líneas de salida. En la tabla, las entradas del decodificador son I0 e I1 y representan un entero de 0 a 3 en código decimal. G es la entrada de habilitación y determina la activación del circuito de acuerdo a su valor lógico ("1" circuito activo, "0" circuito no activo). Según el valor binario presente en las 2 entradas se activa una de las 4 salidas al valor lógico 1. Por ejemplo, con el valor 1 en I0 y el valor 0 en I1 se activará la salida Y1.
G | I1 | I0 | Y3 | Y2 | Y1 | Y0 |
0 | X | X | 0 | 0 | 0 | 0 |
1 | 0 | 0 | 0 | 0 | 0 | 1 |
1 | 0 | 1 | 0 | 0 | 1 | 0 |
1 | 1 | 0 | 0 | 1 | 0 | 0 |
1 | 1 | 1 | 1 | 0 | 0 | 0 |
Tabla. Tabla de verdad del Decodificador de 2 bits
Dibujar el circuito lógico del decodificador 2x4, con entrada de habilitación.
6. El codificador binario 8 a 3 tiene 8 entradas (I0 a I7), una para cada uno de los ocho dígitos y 3 salidas que conforman el número binario equivalente (A0 a A2). La figura muestra el diagrama de bloques del decodificador.
Figura. Codificador binario de 8 a 3
Determinar la tabla de verdad y las expresiones lógicas para A0, A1 y A2. (Sugerencia: construir el circuito con compuertas OR).
Entradas | Salidas | |||||||||
I0 | I1 | I2 | I3 | I4 | I5 | I6 | I7 | A2 | A1 | A0 |
1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
A2=I1 + I3 + I5 + I7
A1= I2 + I3 + I6 + I7
A0=I4 + I5 + I6 + I7
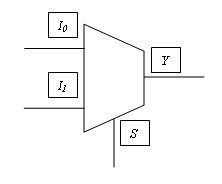
7. El siguiente multiplexor de dos entradas se caracteriza por tener dos líneas de entrada, una línea de selección y una de salida. Su símbolo lógico se muestra en la figura:
Aquí, las entradas son I0 e I1 y la selección es S. El valor de la salida Y depende de los valores lógicos ingresados en los cuadros de texto para las variables I0, I1 y S. Por ejemplo, sí I0=0, I1=1 y S=0, entonces Y=I0=0. La tabla de verdad se muestra en la tabla siguiente.
S | Y |
0 | I0 |
1 | I1 |
Tabla de verdad de un multiplexor de dos entradas
Determinar el circuito lógico correspondiente al multiplexor de dos entradas y una salida (multiplexor 2 a 1).
A | B | Acarreo | Suma |
0 | 0 | 0 | 0 |
0 | 1 | 0 | 1 |
1 | 0 | 0 | 1 |
1 | 1 | 1 | 0 |
8. Determine la tabla de verdad, la ecuación de salida y el circuito lógico de:
a) Un semisumador
b) Un sumador completo
Entradas | Salidas | ||
A | B | Acarreo | Suma |
0 | 0 | 0 | 0 |
0 | 1 | 0 | 1 |
1 | 0 | 0 | 1 |
1 | 1 | 1 | |
A | B | Acarreo entrante | Acarreo saliente | Suma |
0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 1 |
0 | 1 | 0 | 0 | 1 |
0 | 1 | 1 | 1 | 0 |
1 | 0 | 0 | 0 | 1 |
1 | 0 | 1 | 1 | 0 |
1 | 1 | 0 | 1 | 0 |
1 | 1 | 1 | 1 | 1 |
9. Dibuje el circuito lógico de un flip-flop D a partir de un flip-flop RS. La siguiente tabla corresponde a la tabla de verdad de este flip-flop, la cual indica que el dado se transfiere cuando ocurre un pulso de reloj.
D | CLK | Qi+1 |
0 | ↑ | 0 |
1 | ↑ | 1 |
Tabla. Estados del flip-flop D
Describa la forma de operación de este flip-flop.
El flip-flop D (datos) es una ligera modificación del flip-flop SR. Un flip-flop SR se convierte a un flip-flop D insertando un inversor entre S y R y asignando el símbolo D a la entrada única. La entrada D se muestra durante la ocurrencia de uan transición de reloj de 0 a 1. Si D = 1, la salida del flip-flop va al estado 1, pero si D = 0, la salida del flip-flop va a el estado 0.
10. Describa la forma de operación y la tabla de funcionamiento de un flip-flop JK.
Un flip-flop JK es un refinamiento del flip-flop SR en el sentido que la condición indeterminada del tipo SR se define en el tipo JK. Las entradas J y K se comportan como las entradas S y R para iniciar y reinicia el flip-flop, respectivamente. Cuando las entradas J y K son ambas iguales a 1, una transición de reloj alterna las salidas del flip-flop a su estado complementario.
Su unidad básica se dibuja a continuación que, como actúa por "niveles" de amplitud (0-1) recibe el nombre de Flip-Flop JK activado por nivel (FF-JK-AN). Cuando no se especifica este detalle es del tipo Flip-Flop JK maestro-esclavo (FF-JK-ME). Su ecuación y tabla de funcionamiento son:
Q = J q* + K* q











No hay comentarios:
Publicar un comentario